Prof. Kanzieper and collaborators' paper selected as 'Editor’s Suggestion' in PRL

Have you ever played snooker – a game arranged on an elongated, billiard-shaped table? In a recent paper, published in the prestigious Physical Review Letters and highlighted as an "Editor's Suggestion" on the journal website, Prof. Eugene Kanzieper and collaborators – Dr. Roman Riser and Dr. Vladimir Osipov – deal with the billiards, albeit quantum rather than classical.

From the point of view of researchers - mathematicians and physicists – a billiard is a dynamical system in which a particle (ball) moves along a straight line and gets specularly reflected from a wall without loss of speed. The angle of incidence before the collision is equal to the angle of reflection after collision with a wall (the law of reflection). The nature and properties of a ball trajectory is dictated by the law of reflection and by a specific form of a billiard.

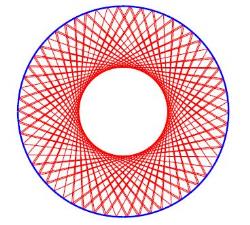
There are two types of billiards: ordered (regular) and chaotic. A shape of an ordered billiard possesses a high symmetry (think of a circle or a square). Following a ball trajectory in an ordered billiard, one discovers that it looks perfectly regular.


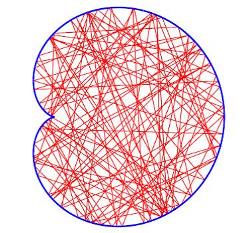
Regular geodesics of a ball in a round billiard	Chaotic geodesics of a ball in a cardioid billiard

On the contrary, a shape of a chaotic billiard – exemplified by a cardioid billiard in the figure above – has a lower symmetry, if any. In this case, a ball trajectory appears to be irregular, and a particle tends to uniformly explore the entire billiard. In addition, a distance between two balls with tiny difference in their initial velocities will diverge very rapidly (exponentially) in time. These two properties are a hallmark of classical chaos.

What will happen if one reduces a billiard size to such an extent that a ball acquires properties of a quantum particle (e.g., starts to behave as an electron described by a wave function)? A similar question: What will happen if one replaces a particle billiard with a wave billiard (e.g., a microwave billiard)? Will it be now possible to determine – through various measurements – whether a quantum (or wave) billiard has an ordered or a chaotic shape? This is one of the major problems in the field of quantum chaos. It is important both theoretically (in quantum mechanics, the Heisenberg uncertainty principle makes the idea of a particle trajectory inappropriate) and practically (modern nanotechnologies make it possible to produce and control quantum billiards).

An illustration of a “quantum billiard"

One of the ways to distinguish between two types of billiards – ordered or chaotic – is to study statistical properties of energy levels of a quantum particle evolving in a billiards. About a decade ago, extensive numerical simulations have suggested that the energy levels in regular quantum billiards produce a noise similar to that of a classical particle performing Brownian motion. In contrast, in chaotic billiards fluctuating energy levels are anticipated to produce a white-like noise.

So far, the results inferred from numerical simulations have not received a satisfactory theoretical explanation. In their paper, Prof. Eugene Kanzieper and his colleagues have used a Random Matrix Theory approach to analyze the noise contained in the spectra of quantum chaotic billiards.

Abstract of the article in English: (https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.118.204101)

Power Spectrum of Long Eigenlevel Sequences in Quantum Chaotic Systems

We present a nonperturbative analysis of the power spectrum of energy level fluctuations in fully chaotic quantum structures. Focusing on systems with broken time-reversal symmetry, we employ a finite-N random matrix theory to derive an exact multidimensional integral representation of the power spectrum. The N→∞ limit of the exact solution furnishes the main result of this study—a universal, parameter-free prediction for the power spectrum expressed in terms of a fifth Painlevé transcendent. Extensive numerics lends further support to our theory which, as discussed at length, invalidates a traditional assumption that the power spectrum is merely determined by the spectral form factor of a quantum system.

This study was carried out in cooperation with Dr. Roman Riser (postdoctoral assistant in the Department of Mathematics at H.I.T.) and Dr. Vladimir Osipov (researcher in the Department of Chemical Physics at Lund University, Sweden and a postdoctoral assistant in the Department of Mathematics at H.I.T. between 2005—2008). The research was supported by the Israel Science Foundation as a part of the project "Bringing the Theory of Integrable Hierarchies to Quantum Chaology" (ISF 647/12).

Published:31.7.2017

Back to all items

Additional programs